[最も好ましい] 三角形 の 底辺 199934-三角形 の 底辺

三角形の角の二等分線と辺の比 三角形ABCにおいて、∠BACを二等分する線とBCとの交点をDとしたとき、次の定理が成り立つ。 このテキストでは、この定理を証明します。 証明 図のように、∠BACの二等分線と辺BCとの交点をDと三角形 底辺の求め方 (小学生) 三角形の高さと面積から底辺を求める方法がわかりません。 面積＝底辺×高さ÷2 高さ＝面積×2÷底辺 上記のように簡単に求められる公式が知りたいです。 よろしくおねがいします。 ちなみに問題は高さ19cm 面積171cm2の三角形A b ×

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角形 の 底辺

三角形 の 底辺-三角形の等積変形 三角形の面積の二等分線 直線の傾き (応用問題) → 携帯版は別頁 == 三角形の面積の二等分線 == 三角形の面積は （面積）＝（底辺）×（高さ）÷2 の公式で求められます． 次の図のように， ABC の頂点 A から対辺 BC の中点（真ん中の点直角三角形の面積を \(S\)、底辺を \(a\)、高さを \(h\) とすると \begin{align}\color{red}{\displaystyle S = \frac{1}{2} ah}\end{align} 直角なので、高さがそのまま辺の長さになるのですね。 例題「直角三角形の面積を求める」 では、実際にこの公式を使って例題を解いてみましょう。 例題 図において、\(\triangle

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

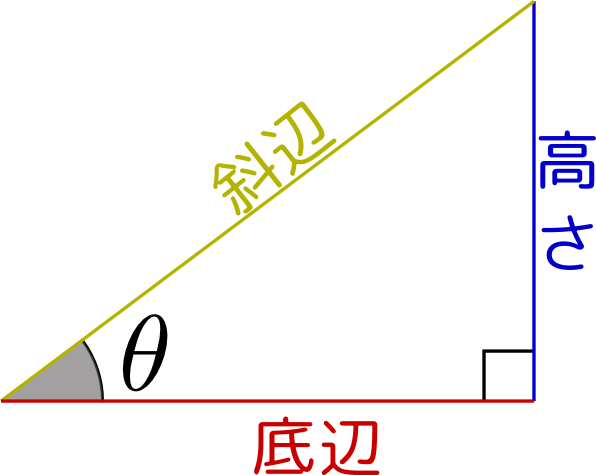
この三角形では、底辺が5㎝、高さを4㎝と見ることができますね。 よって $$\Large{5\times 4\div2=10(cm^2)}$$ となりました。 公式を覚えていれば簡単な問題ですね！ どこを見ればいい！？ 次は、どこを底辺と高さにすればいいのか悩んでしまう問題です。 次の三角形の面積を求めましょう。 この問題底辺 （ていへん）は、 多角形 などの「底部」にある 辺 である。 ただし、 図形 に絶対的な 上下 はないので、紙面や画面上での向きとは無関係に、 計算 などに便利なように底辺を選ぶことができる。直角三角形の三つの辺の名称は「底辺」「高さ」「斜辺」である。 4比とは 比とは、二つ以上の数量の関係を示したものである。 コロン記号「：」を使用して比の関係を表記している。 「a：b=2：1」 の式に込められている情報 aはbの2倍である。 bはaの1/2倍である。 「a：b=4：2」 の

角度 θ(ラジアン)： rad 面積 S： 三角形の計算 ・正三角形(辺から高さと面積) ・正三角形(高さから辺と面積) ・正三角形(面積から辺と高さ) ・直角三角形(底辺と高さ) ・直角三角形(底辺と斜辺) ・直角B = c ×O (0, 0) とすると、直角三角形 A O C の面積は (t a) h 2 、直角三角形 A O B の面積は t h 2 ですから、 A B C の面積は (t a) h 2 − t h 2 = a h 2 となります。 以上により、底辺が a 、高さが h である任意の三角形の面積は a h 2 となることが示せました。

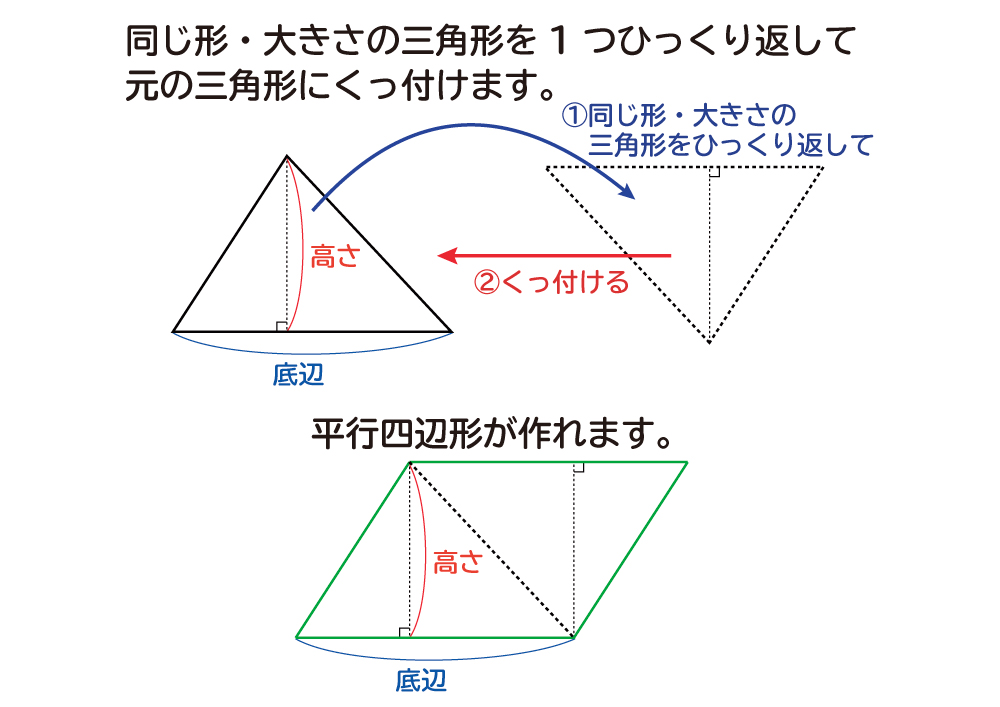
三角形の面積はなぜ底辺×高さ÷2で求められるの？ 三角形は大きく分けて3種類あります。 直角三角形 1 3角形の角のうち1つが90°である三角形のことをいいます。 、鋭角三角形 2 三角形の3つの角、全てが90°より小さい三角形のことをいいます。 、鈍角三角形 3 三角形の角のうち1つのC が成立します。 これを三平方の定理、またはピタゴラスの定理と言います。 例題1： 図のような直角三角形の長い辺の長さを求めよ。 長い辺の長さを c とすると、なぜ、どんな形をした三角形でも、その面積は \(「三角形の面積=底辺×高さ÷2」\) で求まるのでしょうか。 形がちがう2種類の「底辺 \(5cm\) 高さ \(2cm\) の三角形」を通じてみていきましょう。 ※1マス \(1cm\) 初めに、同じ形をした三角形をもう1つ用意します。 それをひっくり返して 重

底辺と角度から 高さを求める ある高さの木から 10m離れて 木のてっ Okwave

三角形の面積を計算する 4つの方法 Wikihow

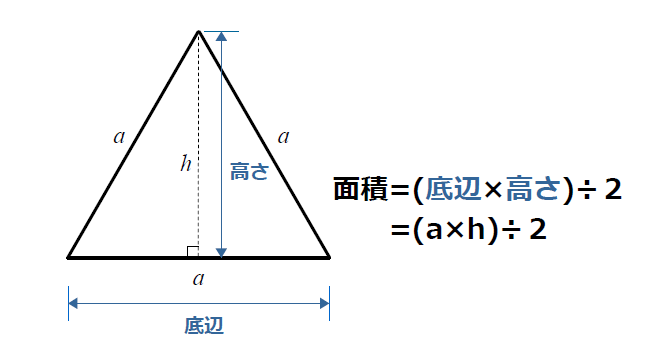
三角形の面積＝底辺×高さ÷2は、直角三角形と鋭角三角形は簡単にイメージできます。 でも鈍角三角形はイメージできませんでした。 他の面積の公式を使用して説明するのも、なんか違うような気がしました。 もっと分かりやすい説明があれば教えてください。 追加：「その2」の説明です三角形の一辺の長さを『底辺』とし、頂点から底辺に向かって垂直に下ろした線の長さを『高さ』と言います。このとき三角形の面積は『底辺×高さ\(÷2\)』で求めることができます。 例題を見てみましょう。 例題 底辺\(6cm\)、高さ\(5cm\)の三角形の面積を求めよ。 答えはこのように求めることが直角三角形の底辺と傾斜角から斜辺と高さを計算します。 底辺 a 角度 θ （525度は 525、5度12分6秒は 5'12'6 と入力） 6桁 10桁 14桁 18桁 22桁 26桁 30桁 34桁 38桁 42桁 46桁 50桁 斜辺 c

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

面積の求め方 計算公式一覧

直角三角形の底辺と角度から、高さ・斜辺・面積を計算します。 底辺と角度を入力し「高さ・斜辺・面積を計算」ボタンをクリックすると、入力された直角三角形の高さと斜辺と面積が表示されます。 底辺a： 角度θ： 度 ラジアン 底辺aが1、角度θが30°の直角三角形 高さ b： 斜辺 c三角形で面積比と底辺の比の関係は？平面図形分野の頻出問題を考える 算数 考え方のポイントは、余計な線分や三角形 を無視して、的確な補助線を引く、ということです。具体的には、下図のようにpとcを結び、 acpと bcpに分割します。 acpの底辺をap、 bcpの底辺をbpとすると、 acpと bcpのこの問題、底辺が10cmで高さが6cmですから「10×6×1/2 = 30cm 2 ！」と答えるのが普通です。しかし、実はこの直角三角形は作れません。なぜ作れないか、以下の図をご覧下さい： 直径10cmの円があります。円の直径と円周上の1

円の特徴 同じ弦をもつ三角形 数学a By Okボーイ マナペディア

正三角形の面積計算 ゆるゆるプログラミング

高さbが1、斜辺cが2の直角三角形 底辺 a： 角度 θ(度)：30 °長い辺（斜辺）を求める方法 直角三角形の直角をはさむ2つの辺の長さを a 、 b として、長い辺の長さを c とします。 このとき、 a ×角度 θ(ラジアン)： rad 面積 S：

Dfrac56timesdfrac14 2 Df Descubre Como Resolverlo En Qanda

三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ

精選版 日本国語大辞典 底辺の用語解説 〘名〙① 三角形の頂点に対する辺。三角形で高さを測るために基準にとった辺。二等辺三角形の等辺でない辺。〔数学ニ用ヰル辞ノ英和対訳字書（18）〕② 物事の底の部分。特に、社会の下層部。※日本の思想（1961）〈丸山真男〉i「近代国家の政正三角形の高さにあたる線を引き、底辺との交点をOとします。 二等辺三角形の性質により、高さにあたる垂線は底辺を二等分するので、直角三角形ABOの底辺は3cmです。 ∠ABOは、正三角形のひとつの角なので60°、よって∠BAOは30°。 つまり ABOは、30°、60°、90°という3つの角で構成された直角底辺aが1、斜辺cが2の直角三角形 高さ b： 角度 θ(度)：60 °

三角形の面積 底辺 高さ 2 をシミュレーションで復習しよう 数学入門

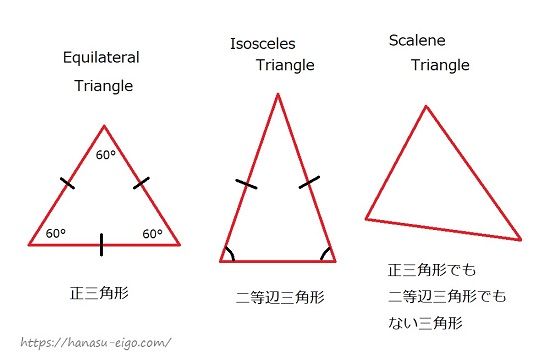
三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

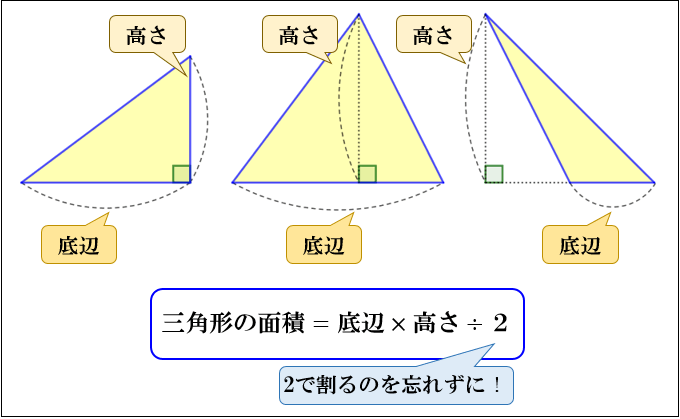
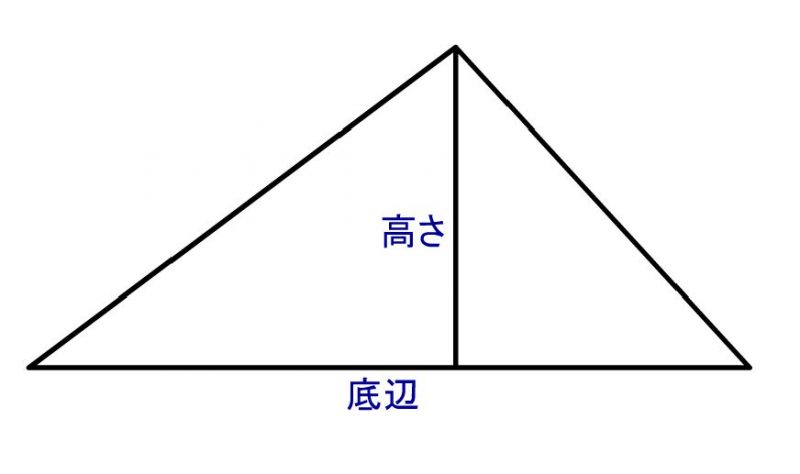
直角三角形の左端の角度が30度の時の比率は次のようになります。 1対2対√3（いったいにたいルートさん） （対辺a＝1、斜辺b＝2、底辺c＝√3） 直角三角形の左端の角度が45度（直角二等辺三角形）の時の比率は次のようになります。二等辺三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と底角 斜辺と高さ 斜辺と底角 高さと底角 面積と底辺 面積と高さ 面積と斜辺 面積と底角 高さ底辺と高さ 底辺は，三角形や平行四辺形などで，高さを測るための基準にとった辺のことをいいます。 高さは，三角形でいえば，頂点からその対辺 (底辺)へ垂直に引いた長さのことをいいます。 したがって，下のように，三角形のどの辺を底辺にとるかにより，高さもそれぞれ異なる位置に表されることになります。

数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三角形の高さの求め方 底辺の位置によって 高さは変わる 中学や高校の数学の計算問題

これで二等辺三角形の底辺の長さを計算できたね！ まとめ：二等辺三角形の底辺は二等分線からはじまる。 二等辺三角形の底辺の計算は簡単。 頂角の二等分線を底辺にひく;・直角三角形(底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します。 ・ 直角三角形(底辺と斜辺) 直角三角形の底辺と斜辺から、高さと角度と面積を計算します。直角三角形の底辺と高さから傾斜角と斜辺を計算します。 底辺と高さから角度と斜辺を計算 高精度計算サイト ゲストさん

三角形の面積を求める方法は何通り その1 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

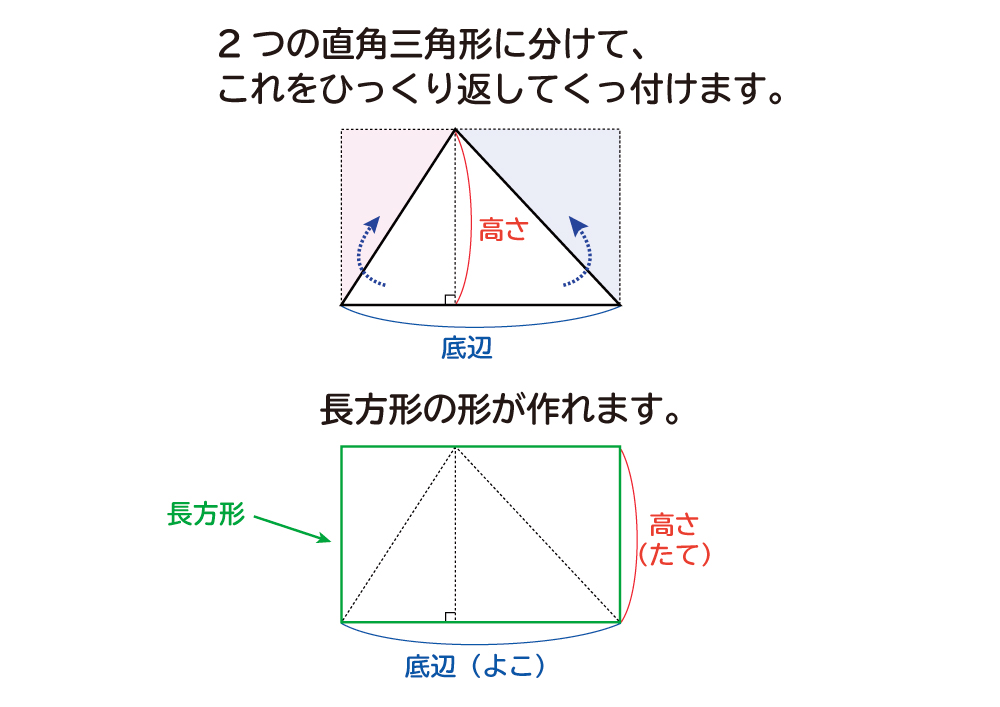
なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

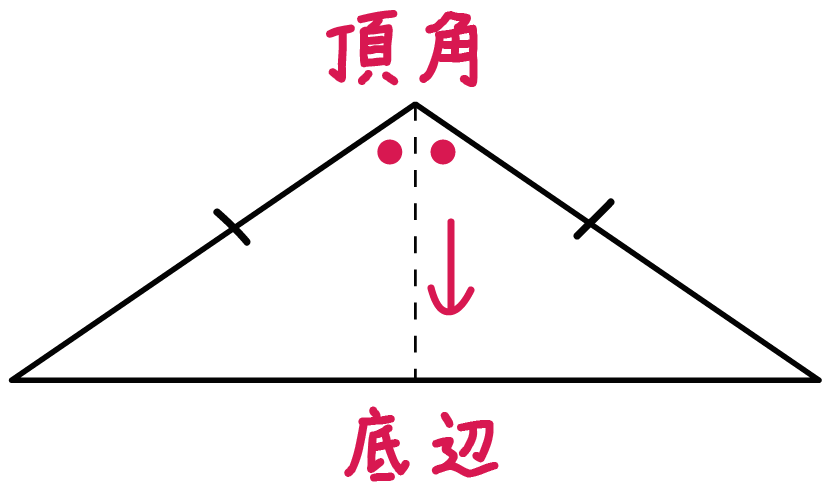
Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos ⁡ θ = a c , sin ⁡ θ = b c , tan ⁡ θ = b a ( 2)三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。二等辺三角形で、長さの等しい 2 つの辺を 等辺 といい、残りの 1 つの辺を二等辺三角形の 底辺 と呼ぶ。 2 つの等辺のなす角を 頂角 といい、残りの 2 つの内角を 底角 という。

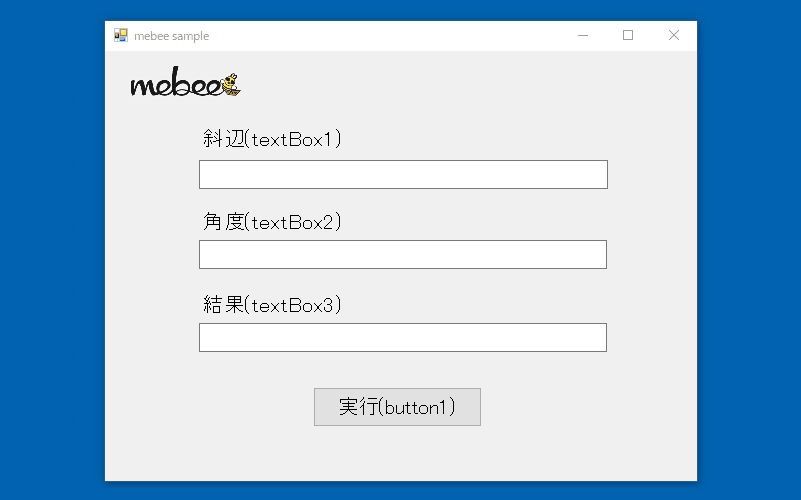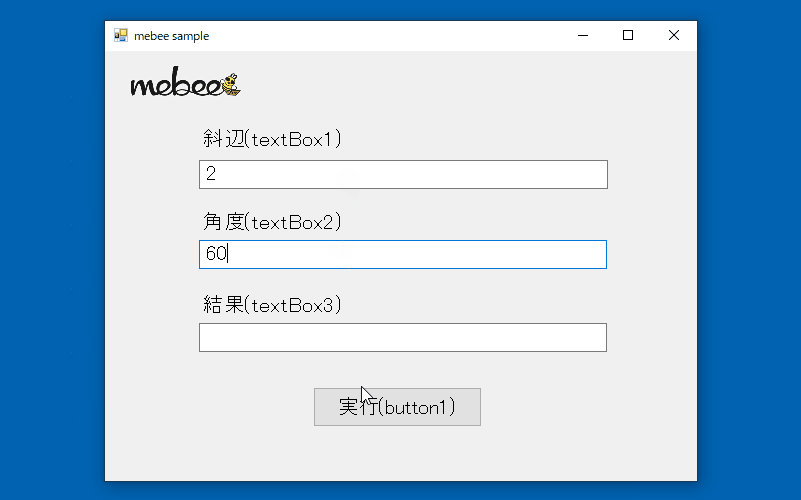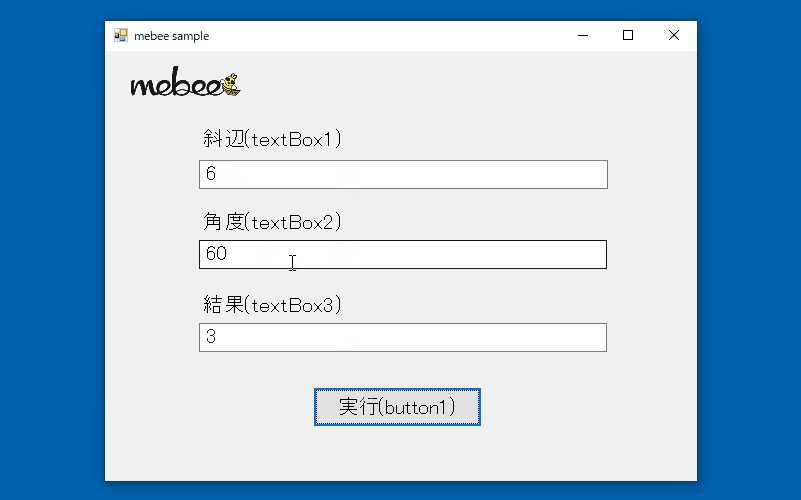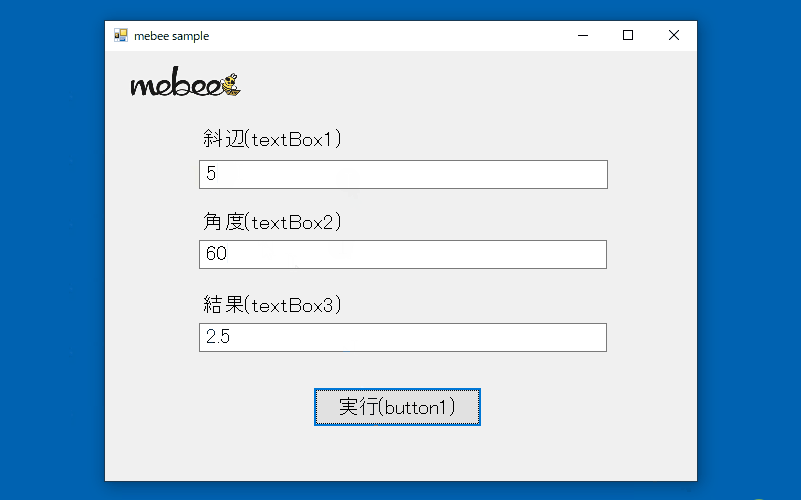
C Cosメソッドを使用して直角三角形の底辺の長さを求める Mebee

第１巻 命題８ 二つの三角形があって ２辺がそれぞれ等しく また底辺が等しかったら それぞれ等しかった２辺に挟まれた角は互いに等しい 数学雑記 楽天ブログ

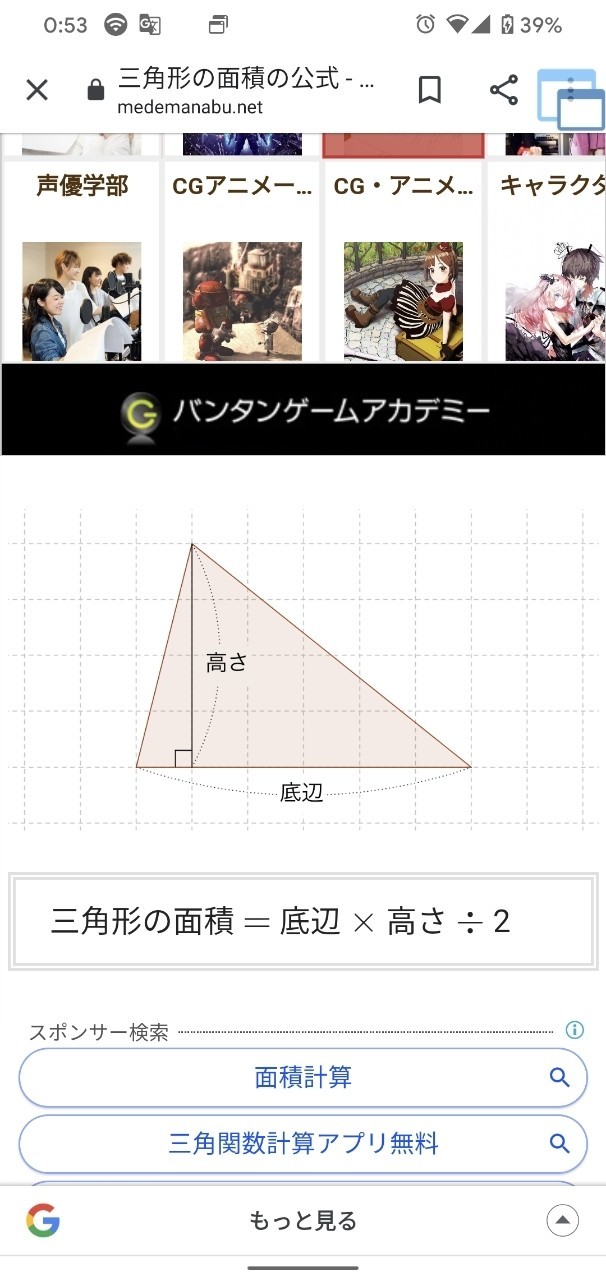
鈍角三角形の面積の求め方がやっと理解できたって話 猿田助 Note

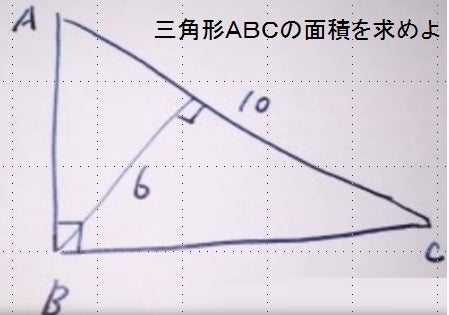
超有名ｉｔ会社入社試験でのひっかけ問題 杉浦技術士事務所のブログ

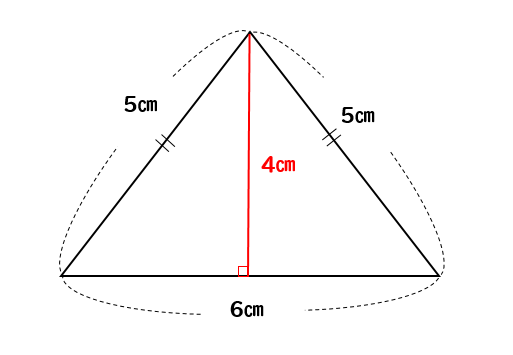
高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

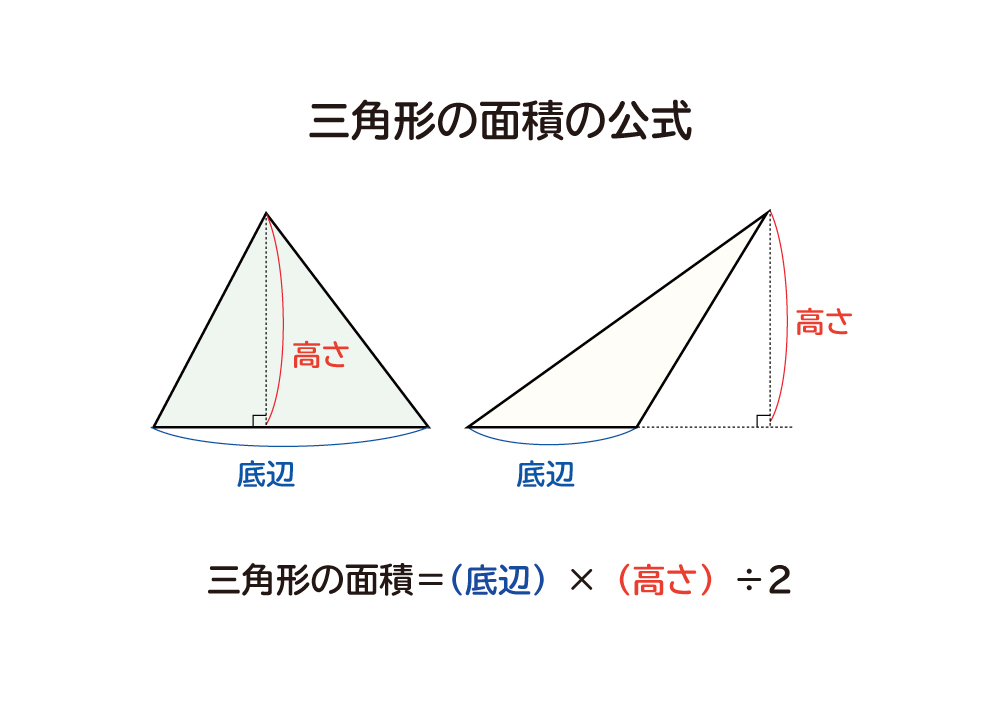
なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

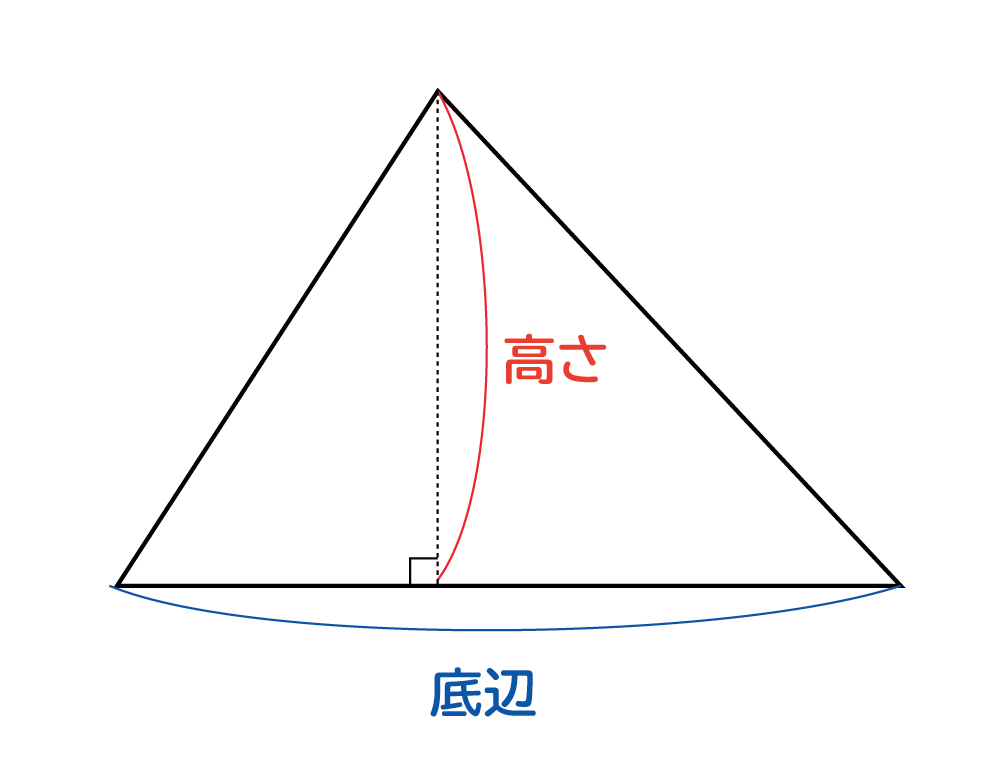
なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

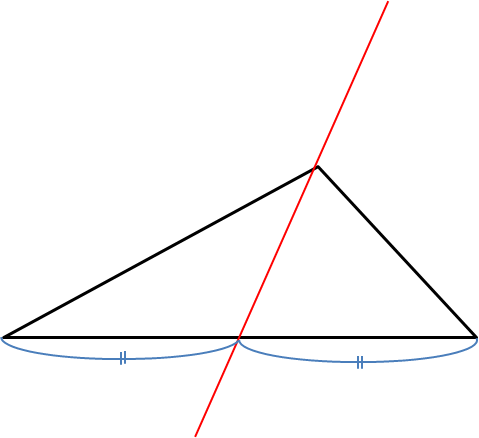
140字で高校受験 数学 頂点を通り 三角形の面積を二等分する直線 とは 底辺の 中点 を通る これは平面図形でも 関数でも用いる考え方 高校受験 数学 T Co 1nfuinsuff Twitter

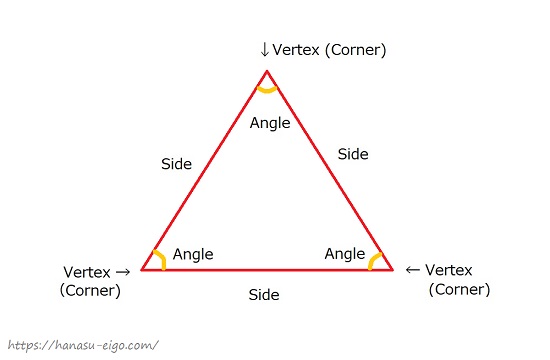
三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

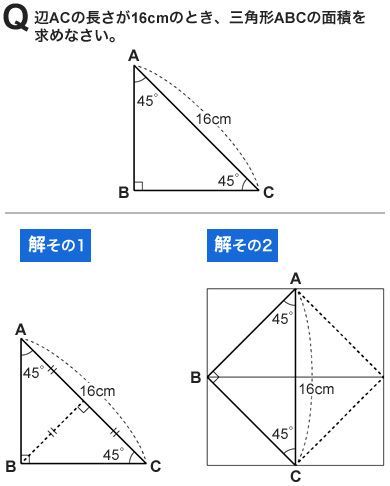
256が解ける子解けない子の差 4つの解法をすぐ思いつくか 2ページ目 President Online プレジデントオンライン

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

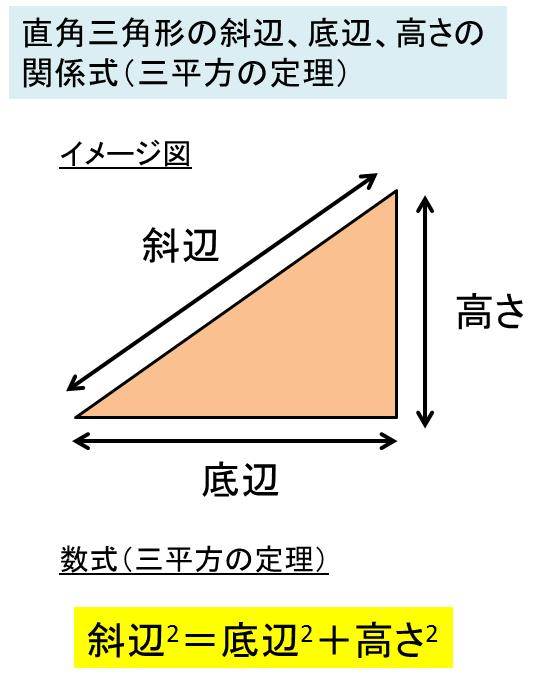
Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方

直角三角形の辺の長さ 合同条件 面積について アタリマエ

直角三角形の角から垂線を引いたときの底辺の比の問題 の裏ワザ 大阪のプロ家庭教師が できない を できる に変える

二等辺三角形の底辺の長さを弦 辺a 辺bの長さを弧とした場合の高さの 数学 教えて Goo

三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

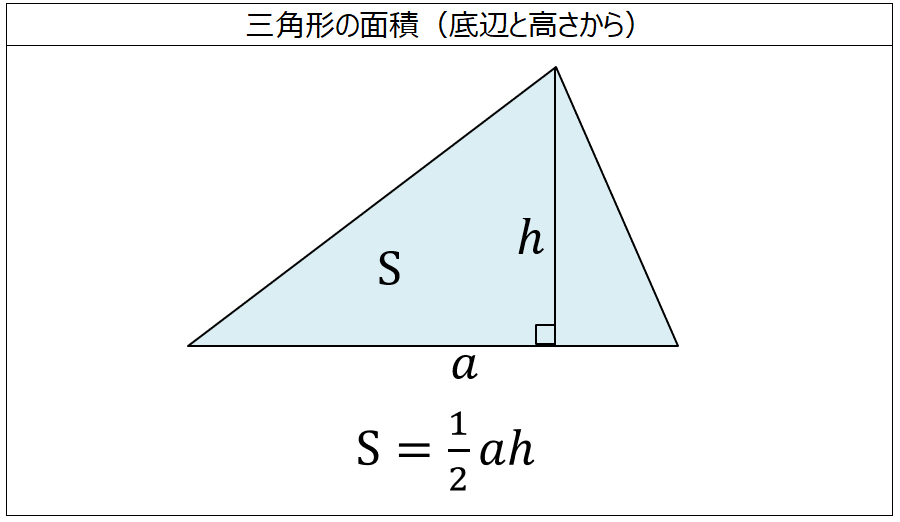
面積の計算 三角形 底辺と高さから 製品設計知識

二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

電験三種の数学 三角比 対辺と底辺の見分け方 電験3種ネット

直角三角形の辺の長さ 合同条件 面積について アタリマエ

直角三角形の計算機 底辺 高さ 面積 角度を計算 かんたん計算機

ベスト三角形 角度 求め方 Tan 最高のぬりえ

Pe10xcm 30 Cm23 Descubre Como Resolverlo En Qanda

マスラボ 小学５年生 三角形の面積 高さや底辺を求める Youtube

三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

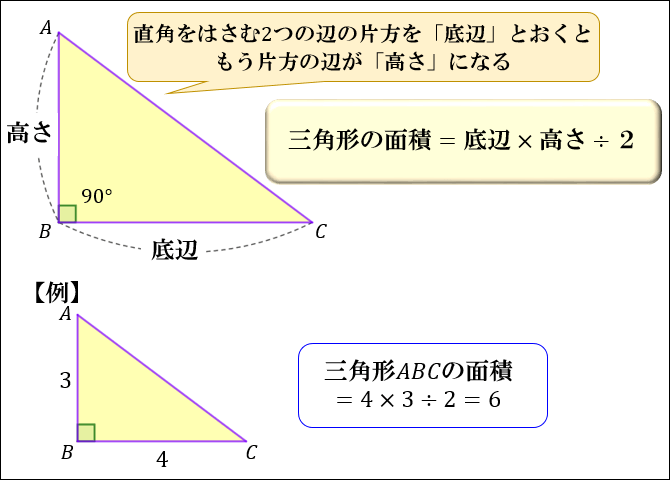
直角三角形の辺の長さ 合同条件 面積について アタリマエ

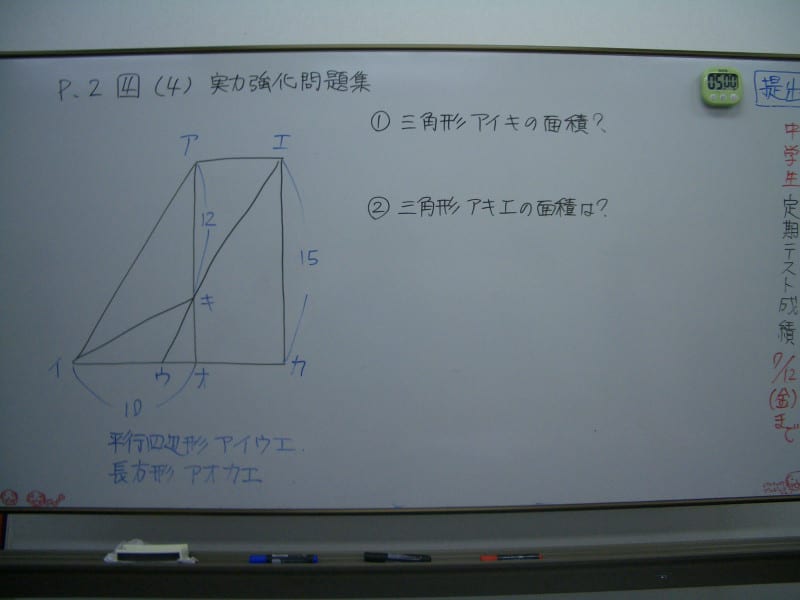
小6算数 三角形の底辺と高さが同じなら 面積は同じ ブログ アビット

三角形の面積比を解説 問題演習で平面図形をマスターしよう 応用編その3 中学受験ナビ

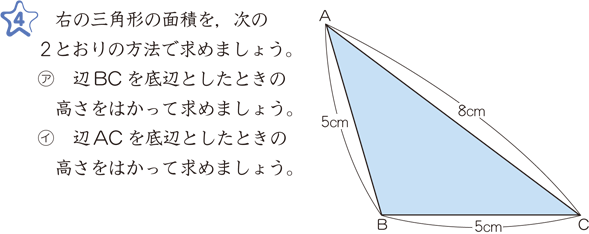
底辺と高さ 算数用語集

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

中学受験算数 チャレンジ 実践問題 三角形の底辺の比と面積 Youtube

三角形の底辺 Triangle08 Twitter

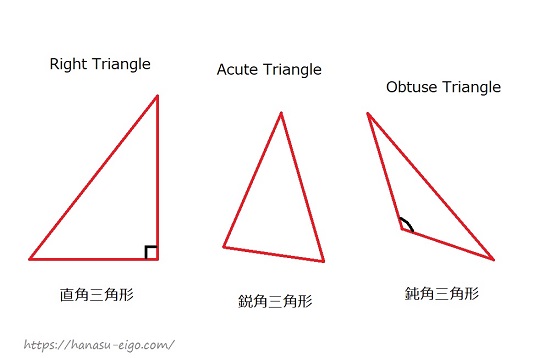
三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

二等辺三角形 ゆるゆるプログラミング

これまでで最高の三角形 の 底辺 子供のための最高のぬりえ

Scm2 Descubre Como Resolverlo En Qanda

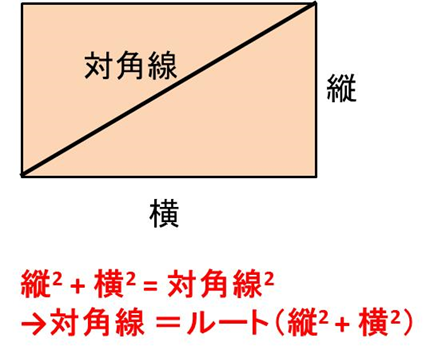
エクセルで対角線の長さの計算をする方法 直角三角形の底辺と高さから斜辺を求める More E Life

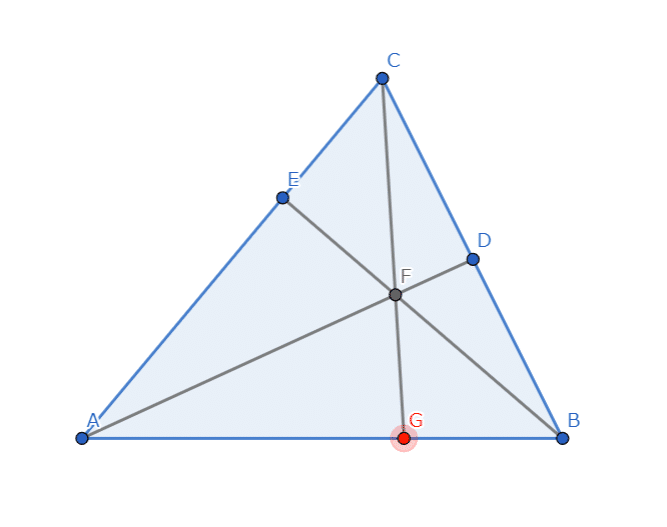
平面図形 三角形を分割した時の底辺の比とコンパスのような部分の面積の比は同じ ワンセンテンス算数 Note

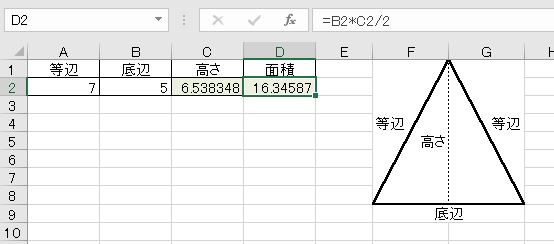
Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

Abac ce Descubre Como Resolverlo En Qanda

三角形の面積の求め方 絶対に覚えておきたい超大切な公式 中学や高校の数学の計算問題

電験三種の数学 三角比 対辺と底辺の見分け方 電験3種ネット

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

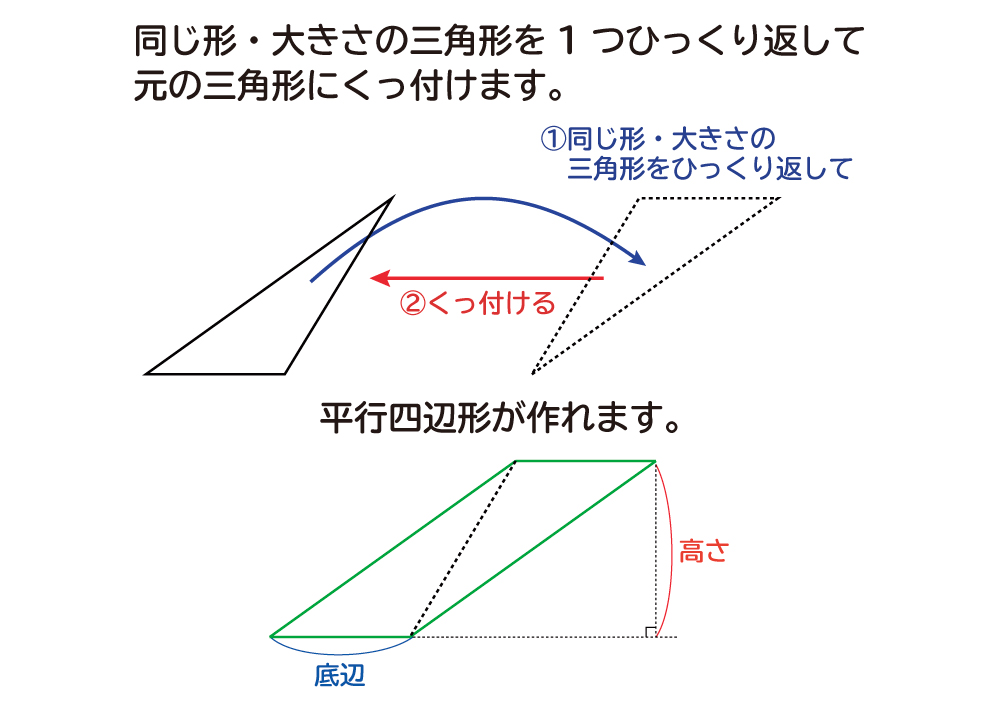
なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める

子どもを混乱させる相似な三角形の２つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生

三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校

Sqrt5 13 See How To Solve It At Qanda

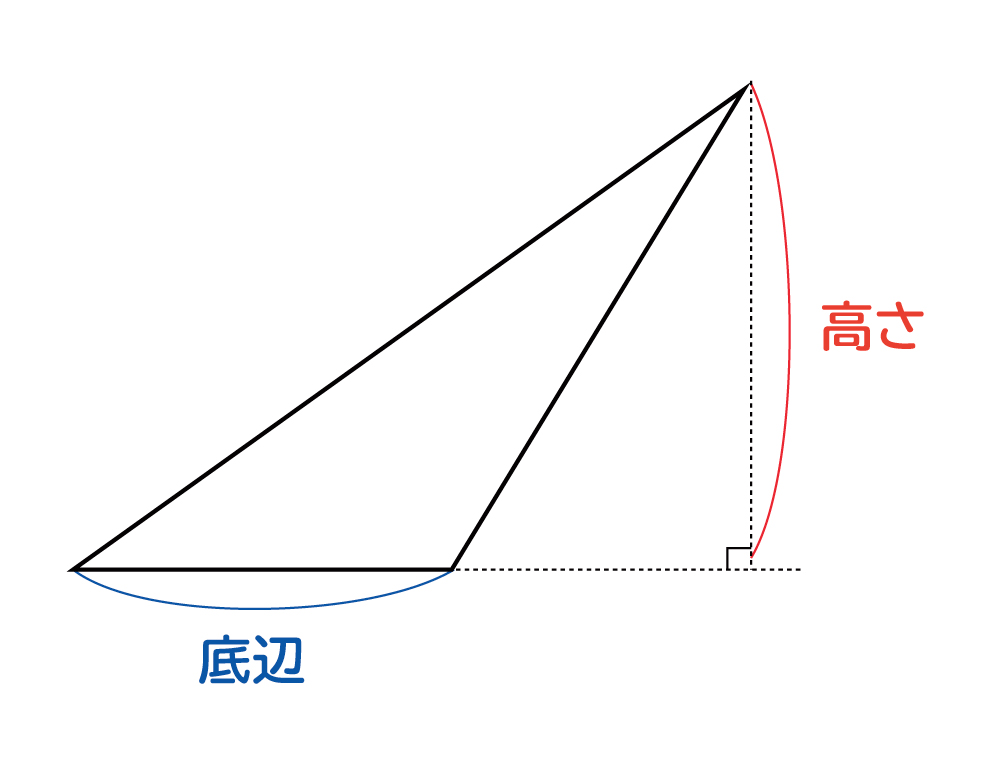
なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

５年算数面積2 教え方のポイント

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張

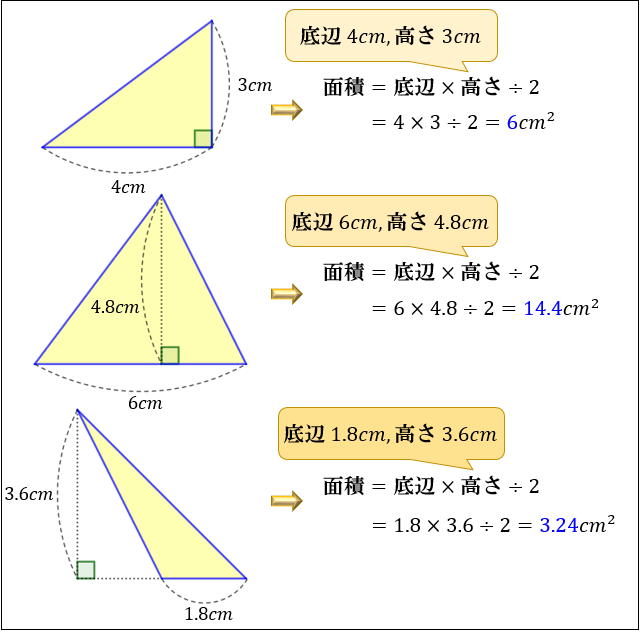
三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ

3 おかしな不等辺三角形 Imujii S Page

三平方の定理と二等辺三角形 Youtube

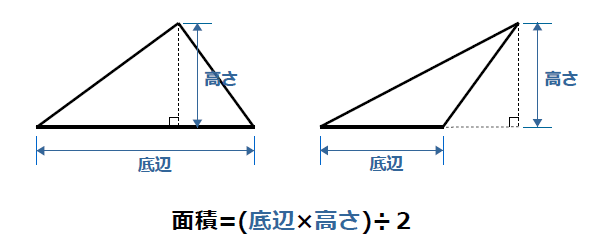
三角形の面積計算 ゆるゆるプログラミング

三角形の高さ あなたは知っていますね 横浜で塾をお探しなら基礎力重視の指導を行う学習塾 ケイスクール

図形の扉 面積のひみつ

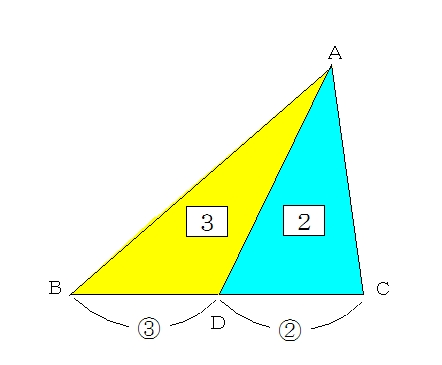
辺の比と面積比

底辺が共通な２つの三角形の角度について ある視覚生理系のテキストの 数学 教えて Goo

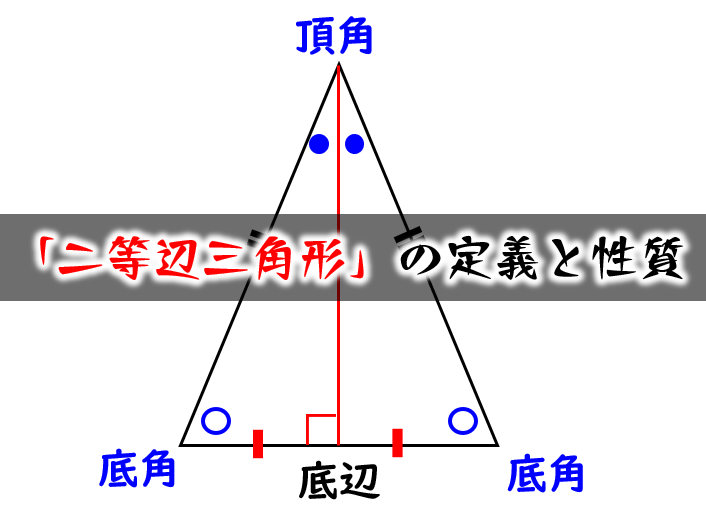
二等辺三角形の定義と性質 問題の解き方 数学fun

二等辺三角形の頂点から下ろした線が底辺の中点を通る時 それは頂角の二等分線であり 底 Clear

三角形の面積比を解説 問題演習で平面図形をマスターしよう 応用編その3 中学受験ナビ

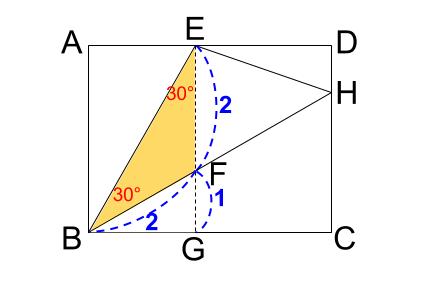
内部底辺の利用 中学数学の無料オンライン学習サイトchu Su

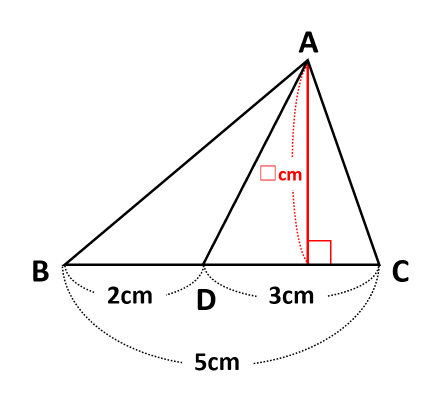
三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ

三角形の面積比を解説 問題演習で平面図形をマスターしよう 応用編その3 中学受験ナビ

勉強しよう数学解答集 三角形の底辺を頂点の足で分割する問題

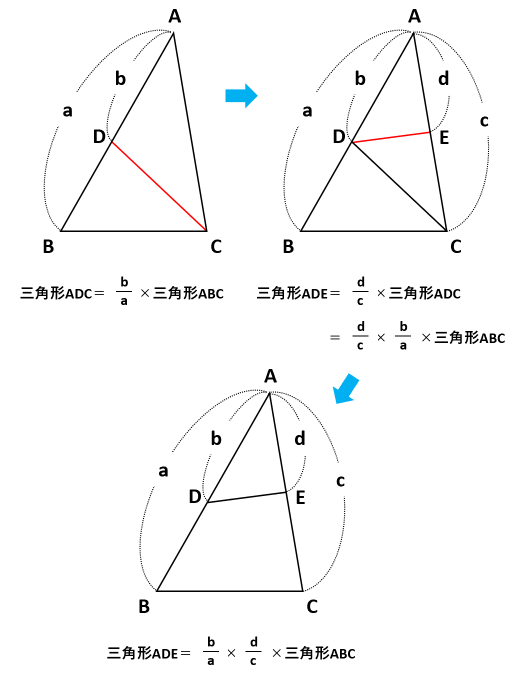
三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ

子どもを混乱させる相似な三角形の２つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生

三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

三角形の面積比を解説 問題演習で平面図形をマスターしよう 応用編その3 中学受験ナビ

頂角が小さい二等辺三角形の底辺について Nano Exit

Math Battle 06 三角形の底辺の中点

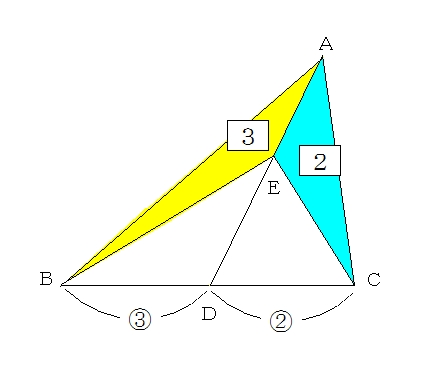
辺の比と面積比

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

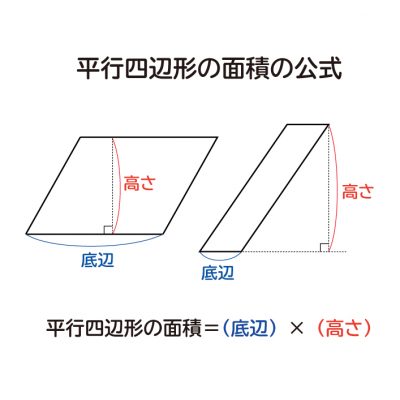
なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

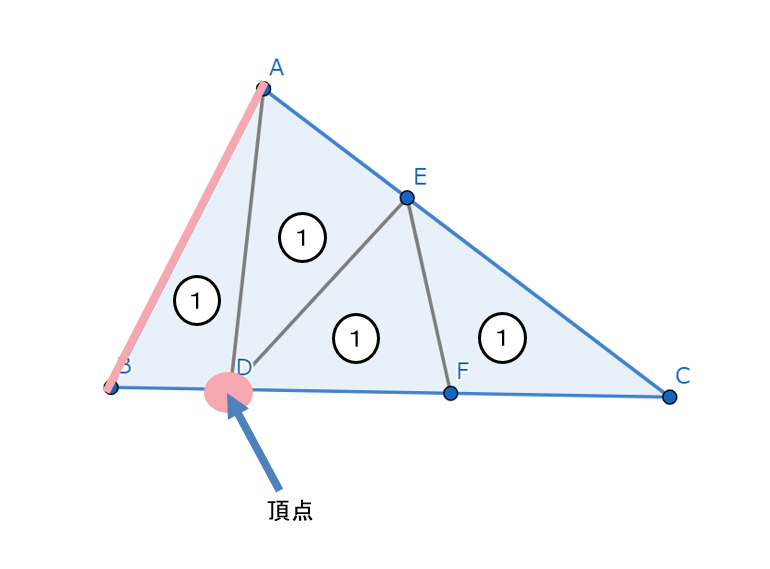
高さの等しい三角形の見つけ方 底辺探し 中学受験プロ講師ブログ

三角形の面積の公式はどうして底辺 高さ 2なのか Irohabook

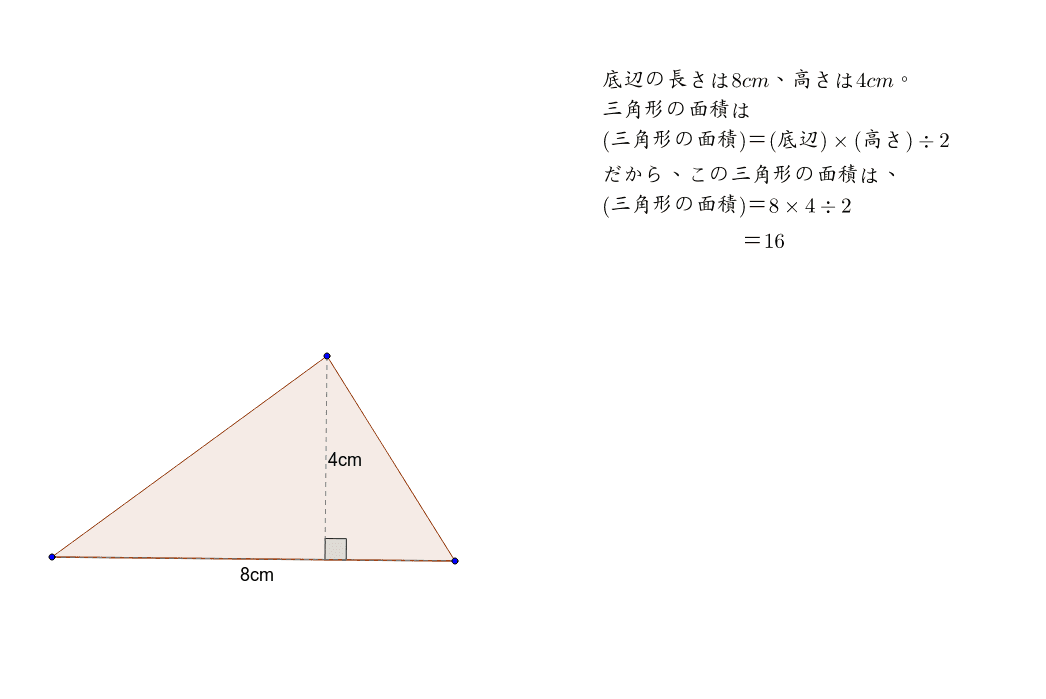
三角形の面積 Geogebra

簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく

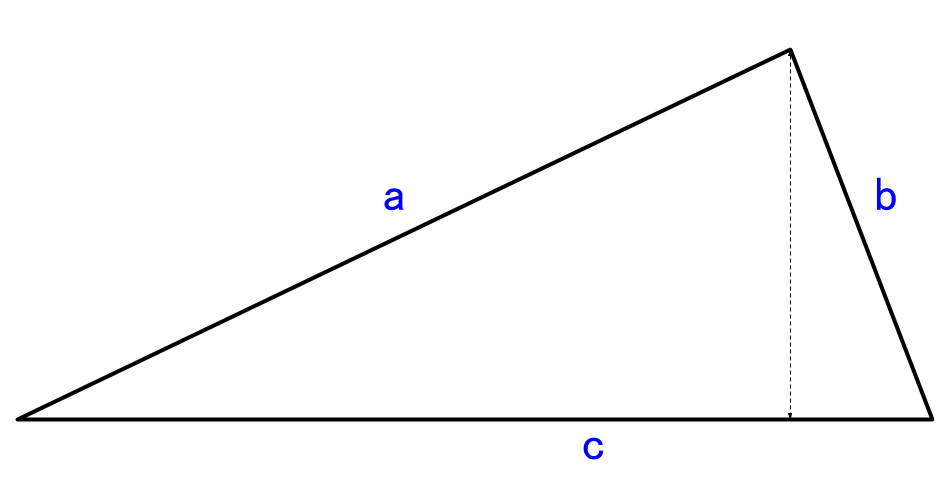
ヘロンの公式 計算機 三角形の面積と高さを 3辺の長さから計算します やまでら くみこ のレシピ

面積が12cm の三角形の底辺xcmと高さycm この下の図と上の問題で質問で 中学校 教えて Goo

Incoming Term: 三角形 の 底辺,